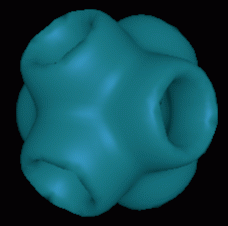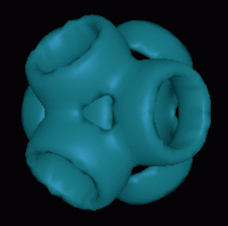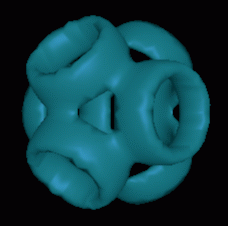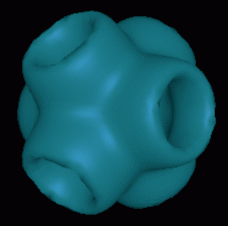
Figure 1: An Example of Ray-Quadric Shapes.

By using these operators over the the ray-linear formulas that represent star solids with the same center, we are able to construct ray-quadric representations of toroids and solids with many holes. Since they provide a large variety of shapes, intuitive shape construction, real-time rendering and interactive shape design, ray-quadrics are suitable for use as building blocks in implicit-equation-based modeling tools such as Constructive Solid Geometry and soft objects.

Introduction

A modeling tool that capitalized on the different strenghts of both implicit and parametric techniques would greatly extend the power of geometric modeling tools. Such a tool could be used as a building block for implicit representations because of its implicit properties, while also providing fast and simple rendering because of its parametric properties. In fact, quadrics and superquadrics, both of which are popular mathematical tools in computer graphics, provide both representations. In this paper, we introduce another mathematical tool that has such a dual nature: ray-quadrics. Ray-quadrics, like hyperquadrics, are a superset of superquadrics. Whereas hyperquadrics generalize superquadrics by going to higher-dimensions, ray-quadrics arise by introducing non-homogenous functions. But, as we shall see, they behave like homogenous functions in a sense that will become clear. The modeling properties of ray-quadrics can be summarized as follows:

1. Design: A subset of ray-quadrics can be constructed by using geometric operators over ray-linears. This new set of operators provides exact and approximate set difference, border-intersection and flesh operation. By using these operators over the ray-linear formulas of star shapes with the same center, ray-quadric representations of toroids and shapes with many holes can be constructed.

   Ray-linear representations of half-spaces that include the origin provide the simplest construction primitives (building blocks). By using the approximate intersection and union operators of Ricci ray-linear representations of convex and star shapes with the same center can be constructed from ray-linear formulas of half-spaces. The approximate union and intersection operations can be considered global blending operations. These operations over non-negative ray-linear representations of half-spaces are closely related to the super-elliptic local blending of Rockwood. As a result, ray-quadric representations provide simple and intuitive operations.

2. Control: Exact set operations over half-spaces result in control shapes for ray-quadrics. Since the control shapes we use for ray-linears are star polyhedra, the control shapes for ray-quadrics would be two star polyhedra with the same center.

3. Computation: Ray-quadrics are similar to ray-linears: their intersections with a parametric equation of a ray that starts from the origin simplify to quadrics. In fact, this simplification phenomenon suggests the name {\em ray-quadric}. Because of this simplification, ray-quadric implicit forms can easily be parameterized like ray-linears. Therefore, once the related parametric equations are obtained, computing the shapes is simply the evaluation of the related parametric equations.

4. Organic Appearance: Control of organic appearance is accomplished by changing blending parameters. These blending parameters smooth out the sharp edges and corners resulting from exact set operations. There are four types of blending parameters: global (union), local (intersection), set-difference and flesh. The global blending parameter smooths out sharp edges resulting from the exact union of convex polyhedra. Blobby effects come mostly from this global blending parameter. Local blending parameters smooth out sharp edges and corners of convex polyhedra that result from the intersection of half-spaces. Different combinations of global and local blending parameters create different looks. Generally speaking, we can say that more blended shapes look fleshier, whereas less blended shapes look more robotic and less organic. The set difference operator smooths out sharp edges resulting from the exact set-difference of two star polyhedra. The flesh operator creates a flesh around the space curves generated by the border-intersection operator.

Conclusion and Discussion

We introduced a new building block for implicit representations: ray-quadrics. Ray-quadrics provide a large variety of shapes with intuitive shape construction, real-time rendering and interactive shape design. In order to represent shapes that cannot be represented by a single ray-quadric formula, ray-quadric formulas can be used in constructive solid geometry or in Blinn's exponential functions in the form of or in the soft object equations. Ray-quadrics can be deformed by using deformations or superposed by using convolution}. Higher-degree ray-polynomials can also be used to represent shapes that cannot be represented by a single ray-quadric formula. For instance, it is possible to represent a teapot with only one ray-cubic inequality. The main problem is in finding intuitive geometric operators which give higher-degree ray-polynomials. In addition, rendering will not be as easy as for ray-quadrics. It seems that these two problems may limit the usage of ray-polynomials to ray-quadrics.

Acknowledgments

I would like to thank to Graphics, Visualization and User interface Center at Georgia Tech and Computer Science Department at Yildiz Technical University. I also would like to thank Lambert Meertens, Donald House and Jason Rosson for their helpful suggestions.