Introduction

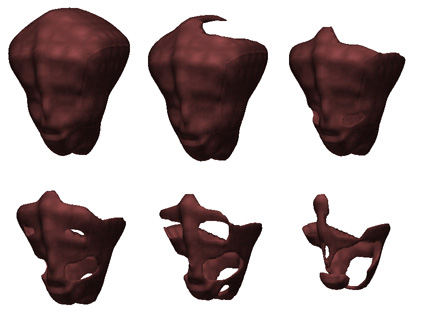
Figure 1: Interactively Generated Ray-Quadric Shapes.

The key problem in developing a sculptor-friendly shape modeling system comes from the restrictions imposed by the commonly used tensor-product B-spline parametric forms. Since B-splines can provide interactive shape construction and easy implementation, they are extremely attractive for the designers of solid modeler designer systems. However, since the control point mesh of tensor-product B-splines must be organized as a regular rectangular structure, they can only support surfaces with limited topology. For modeling surfaces of arbitrary topology with B-splines a number of techniques have been advanced. Forsey and Bartels proposed Hierarchical B-Splines, Loop and DeRose introduced S-patches for generalization of B-spline surfaces to support arbitrary topologies, Loop later introduced quad-nets to refine irregular meshes and Grim and Hughes used manifolds for modeling surfaces of arbitrary topology.

Subdivision surfaces first proposed by Catmull and Clark offers an non-analytical alternative, and overcomes the topological restrictions of the tensor product B-splines. However, subdision surfaces do not allow topological change during construction.

The most powerful mathematical tools for representing and changing arbitrary topologies are implicit surface representations such as Soft-Objects, Constructive Solid Geometry, F-representations, Hyperquadrics, Ray-quadrics and others. The major obstacle for some implicit representations lies in computation time. The problem is that more complicated shapes require a larger system of implicit formulas. This usually results in more computations due to the increased size of the implicit formula. Ray-quadrics is not an exception. A general ray-quadric formula can be extremely hard to compute. However, for a certain subset of ray-quadrics the computation time remains constant, completely independent of shape complexity. Moreover, this constant computation time is small enough to permit interactive shape construction. Thus, a subset of ray-quadrics guarantees interactive computation.

Another advantage of ray-quadrics is that their topological limitations are different from those of tensor product B-splines. Ray-quadrics can only represent surfaces that satisfy the ray-quadric condition. A surface satisfies the ray-quadric condition if there exists a point such that every ray originating from this point intersects the surface at at most two points. This condition can be considered an important compromise for many shape modeling applications. However, for some other applications such as sculpting faces, ray-quadrics can be extremely useful. Faces have just such handles (or holes) - the mouth, nostrils, eyes and so on - and can be topologically represented by toroids with several handles. If we exclude the ears, for most faces it is possible to find a point such that every ray originating from this point intersects the face at {\em at most two} points, which is exactly like a surface that satisfies the ray-quadric condition.

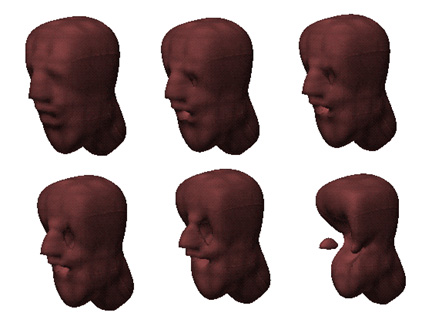
Figure 2: Interactively Generated Ray-Quadric Shapes.

Ray-quadrics had two earlier problems that limited their use. First, the mathematical description of ray-quadrics was too complicated. Ray-quadrics are a subset of a class of functions called ray-polynomials. We have recently developed a more intuitive mathematical formulation which relates ray-polynomials with univariate quadratic equations. The new formulation based on ray-polynomials simplifies working with ray-quadrics and the development of software based on ray-quadrics. Second, polygonization of ray-quadric surfaces was not intuitively simple. By introducing the concept of dummy intersection points, the polygonization process has become more intuitive. We have developed prototype software for interactive shape modeling based on these new approaches. The shapes shown in Figures 1 and 2 are constructed interactively by using this prototype system.

Future Work

Our prototype system has several limitations imposed by our user interface design. However, despite its limitations, this prototype ray-quadric shape modeling system shows the viability of ray-quadrics as a computer aided shape modeling tool. Its user interface can be improved into a more intuitive one by restricting ourselves to special kind of objects such as faces.

We have shown that feature based templates can provide an intuitive user interface for facial modeling. Set-operation based construction of ray-quadrics solids is suitable for developing feature based user interfaces for modeling faces. In such a system, the sculptors can simply draw the polygonal facial features for front and side views of the face and the system can automatically construct the facial solid from the front and side views. Development of such a system requires methods to find the control shapes from described features. As a future work, we are planning to develop a ray-quadric based facial modeler.

When ray-quadrics are used in facial modeling, they can provide additional advantage. Facial data may be greatly reduced by using Ray-quadric representations. The user can save the data as a template. The template will actually be the coefficients of the ray-quadrics equations. At most seventy integer coefficients between 0-128 are enough to represent the faces shown in Figures 1 and 2. These coefficients are extremely robust; in other words, the resulting shape is only slightly effected by small changes in the coefficients.

Acknowledgments

We would like to thank to Donald House, John Ferguson, Lori Cagle and refeerees for their helpful suggestions. We also thank Dietmar Saupe for the initial spark for the new formulation.