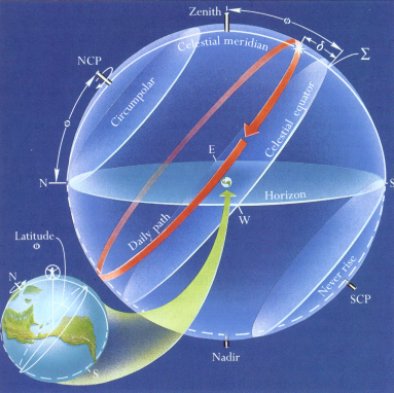
The celestial sphere

The sky above the horizon appears to us as a hemisphere. The zenith (Z) is straight up. (The nadir is opposite the zenith, under your feet on the other side of the Earth.) In the northern hemisphere the sky appears to turn counter-clockwise around the North Celestial Pole (NCP), which is very close to the star Polaris. The cardinal points on the horizon are the north point (N), the east point, the south point (S), and the west point (W). The celestial meridian is an imaginary line in the sky that extends from the north point on the horizon, through the NCP, through the zenith, and to the south point on the horizon. It divides the sky into an eastern half and a western half.
If we passed a plane through the Earth's equator and extended it to the celestial sphere it would trace out the celestial equator. Just as every point on the Earth's equator is 90 degrees from the north and south geographic poles, every point on the celestial equator is 90 degrees from the North and South Celestial Poles.
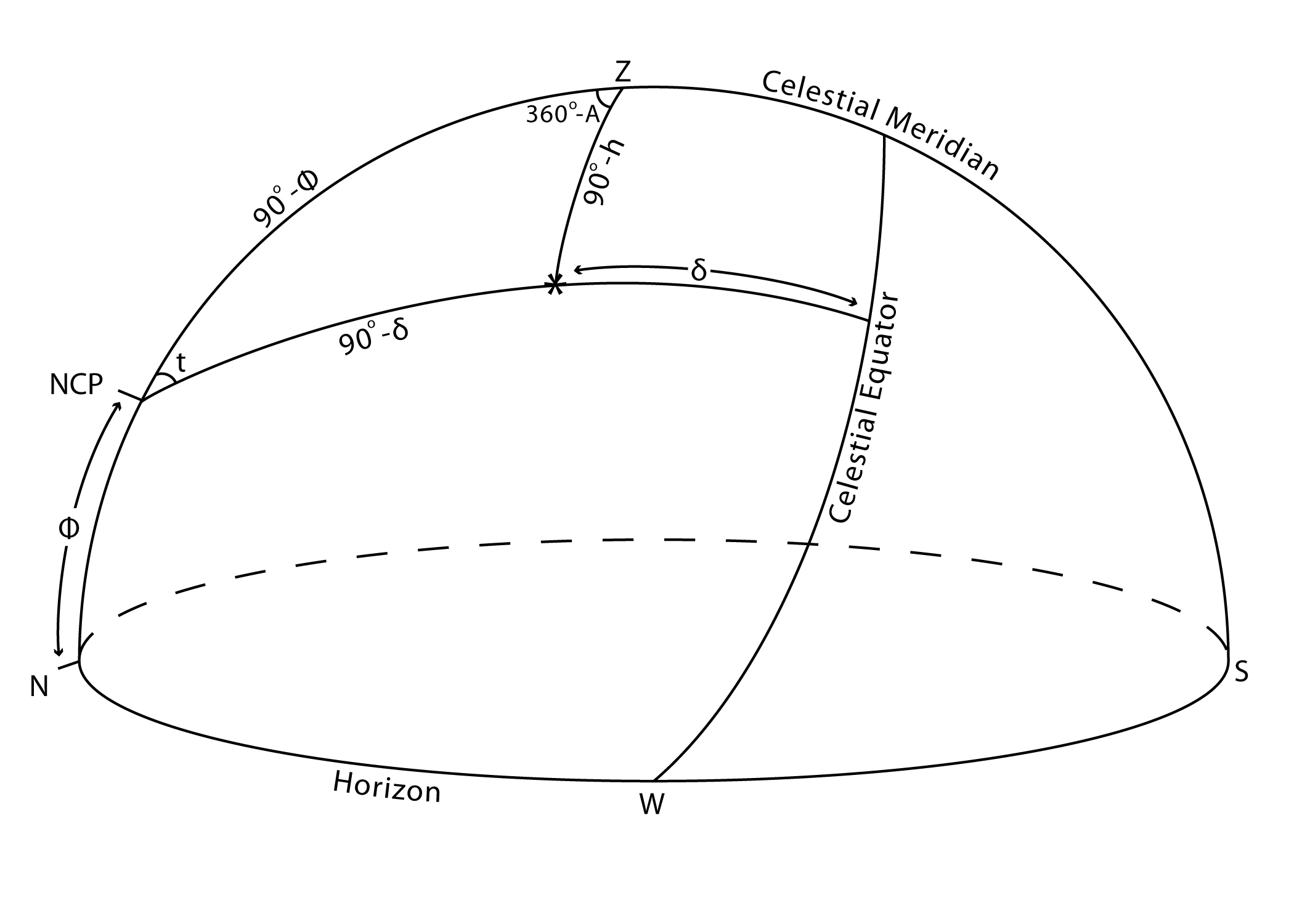
Consider a star in the western half of the sky, as shown. The declination (delta, or DEC) is equal to the number of degrees north or south of the celestial equator that the star is located. The elevation angle (or altitude) of the star (h) is the number of degrees that the star is above the horizon. The hour angle is the number of degrees that the star is east (negative) or west (positive) with respect to the celestial meridian. Imagine a great circle from the zenith, through a star, and extended to the horizon. From the north point on the horizon, clockwise around the horizon to this point is called the azimuth of the object.
For our purposes here we can consider the latitude of any given geographic site as a constant. Likewise, from night to night the declination of a star is essentially constant. However, because of the rotation of the Earth, the elevation angle, azimuth angle, and hour angle of a star change continuously. This requires us to use a special mechanical mounting, or a computer controlled mounting to guide on a star when observing it with a telescope. Otherwise the stars just drift through the field of view.
In the horizon system of astronomical coordinates we specify the position of an object in the sky by its elevation angle (h) and azimuth (A).
The ecliptic is the apparent path of the Sun around the Earth over the course of the year. It is a great circle inclined 23.4 degrees to the celestial equator. Over the course of the year the declination of the Sun changes from -23.4 deg on December 21st, to +23.4 deg on June 21st. As the Sun crosses the celestial equator going from south declination to north declination, we call this moment the vernal equinox or first moment of spring. It is also a direction in the sky known as the First Point of Aries. (Presently, that point on the sky is in the constellation Pisces. Soon it will shift to the constellation Aquarius. Then it will be "the dawning of the Age of Aquarius" as in the song from the musical Hair!)
A good system of astronomical coordinates is the equatorial system. Just as one's location on Earth can be specified by one's latitude and longitude, a star's coordinates in a (nearly) fixed frame of reference are called the declination DEC) and right ascension (RA). The RA is the number of degrees (or alternatively - hours, minutes, and seconds) that a star is east of the vernal equinox (RA = 0, DEC = 0). DEC, as mentioned above, is the number of degrees that a star is north or south of the celestial equator. You can look up the coordinates of a star in a star atlas and get its RA and DEC. To calculate the elevation angle and azimuth, you would also need to know the date, the time, and your latitude and longitude.
For an object like the Sun or Moon that always cross the meridian south of the zenith for observers at mid-northern latitudes the maximum elevation angle of the object is equal to:
h_max = 90 - phi + delta
From the law of cosines in spherical trigonometry it is easy to show that
sin(h) = sin(phi) sin (delta) + cos(phi) cos(delta) cos(t)
From the law of sines in spherical trigonometry it is easy to show that
sin(360-A) / sin(90 - delta) = sin(t) / sin(90 - h), or
sin(A) = - sin(t) cos(delta) / cos(h)
Go back to Kevin Krisciunas home page by clicking here.