How_to_prepare_6N_NaOH (Sodium Hydroxide)
6N NaOH = 6M NaOH 6M NaOH are 6 moles in 1L MW (NaOH) = 39.88 gr/mole so: m = n x MW = 6 x 39.88 = 239.28 gram NaOH.
1 M HCl = 1 N HCl (36.5 gram/L)
Calculations Using Molarity Page 1 of 4
According to the international SI unit use the following equation:
Calculated osmolarity = 2 Na + Glucose + Urea (all in mmol/L).
or
Calculated osmolarity = 2 Na + 2 K + Glucose + Urea (all in mmol/L).
Most covalent compounds do not dissociate or ionize in water. However, an ionic compound separates into cations and anions on dissolving. In some chemical processes it is important to know the concentration of the total number of particles dissolved in solution. This is where the concentration unit osmolarity is useful. The osmolarity of a solute in solution refers to the Molarity of the compound x the number of particles produced per mole of compound when it dissolves in water.
Example 8:
What is the osmolarity of a 1.0 M solution of ethyl alcohol (C2H6O) in water? Ethyl alcohol is a covalent compound that does not ionize in water. Each mole of C2H6O which dissolves produces only one mole of particles. So, osmolarity = 1.0 M x 1 mole of particles/mole compound = 1.0 osmol C2H6O.
Example 9:
What is the osmolarity of a 1.0 M solution of CaCl2? When 1 mole of CaCl2; CaCl2 --> Ca+2 + 2 Cl-. So, osmolarity = 1.0 M x 3 moles ions/mole compound = 3.0 osmol CaCl2
Use sucrose (glucose) to increase osmolarity, and distilleddeionized water (e.g., from a MilliQ system) to reduceosmolarity. Sucrose isn't charged, so you don't have to worryabout it messing with your reversal potentials, etc. It's alsonot a salt, so 1 mM of sucrose increases osmolarity by 1 mOsmol.
• = 2[Na+] + [Glucose]/18 + [ BUN ]/2.8[5] where [Glucose] and [BUN] are measured in mg/dL.
Simplifications are sometimes used:[6]
• = 2[Na+] + [Glucose]/20 + BUN/3 – 2
6N NaOH = 6M NaOH 6M NaOH are 6 moles in 1L MW (NaOH) = 39.88 gr/mole so: m = n x MW = 6 x 39.88 = 239.28 gram NaOH.
1 M HCl = 1 N HCl (36.5 gram/L)
Calculations Using Molarity Page 1 of 4
There are several types of calculations that you need to be able to do with molarity.
First, you should be able to calculate the molarity if you are given the
components of the solution.
Second, you should be able to calculate the amount of solute in (or needed to make) a certain volume of solution.
Third, you might need to calculate the volume of a particular solution sample.
Fourth, you might need to calculate the concentration of a solution made by the dilution of another solution. This and related calculations will be covered in a separate page.
In either of the first two cases, the amount of solute might be in moles or grams and the amount of solution might be in liters or milliliters. Please note that with molarity we are concerned with how much solute there is and with how much solution there is, but not with how much solvent there is.
The examples that follow are also shown in example 3 in your workbook. You may want to look through the workbook examples on your own and if they make perfect sense to you, test your understanding by doing exercise 4. Then check your answers below before continuing on to dilution calculations.
Here is the general relationship that you
will be using over and over again. The
molarity is equal to the number of moles of
solute divided by the volume of the
solution measured in liters. If you like to
think of numbers and units instead of
quantities look at the second version of the
equation. In this equation x, y and z
represent numbers: 2, 6 and 3 for example.
1/7/2011
http://dl.clackamas.edu/ch105-04/calculat.htm
Calculations Using Molarity Page 2 of 4
Here we are given something to figure out. To get the molarity we need to divide the number of moles of NaCl by the volume of the solution. In this case that is 0.32 moles NaCl divided by 3.4 L, and that gives 0.094 M NaCl.
This one is a bit more difficult. To get molarity we still need to divide moles of solute by volume of solution. But this time we're not given the moles of solute. We have to calculate it from the mass of NaCl. We multiply 2.5 g NaCl by the conversion factor of 1 mole NaCl over the formula weight of NaCl, 58.5 g. That tells us that we have 0.0427 mole of NaCl. I kept an extra digit here because we are not done with the calculations. When we are done I'll round off to two digits, the same as in the 2.5 g weight of NaCl. Now that we know the moles we can calculate the molarity. Moles of solute (0.0427) divided by the volume of the solution (0.125 L) gives us 0.34 M NaCl.
This question asks how you would prepare 400. ml of 1.20 M solution of sodium chloride. In this case what you need to find out is how much NaCl would have to be dissolved in 400 ml to give the concentration that is specified. This amount is going to have to be in grams because we don't have any balances that weigh in moles. So there
is more than one step to this problem.
The approach shown here is a conversion factor approach. It involves remembering that molarity is a relationship between moles and liters. 1.20 M NaCl means there is 1.2 moles of NaCl per 1.00 liter of solution. We can use that as a conversion factor to set up the calculation that relates
400. ml (or .400 L) to the appropriate number of moles of NaCl. So we take .400 L and multiply by the conversion factor to
http://dl.clackamas.edu/ch105-04/calculat.htm
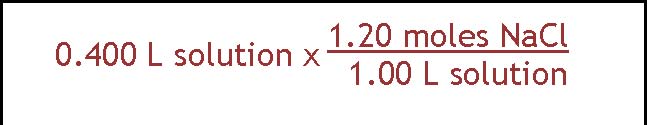
Calculations Using Molarity
get .480 moles NaCl. The next step is to find out how many grams that is. We change from moles of NaCl to grams by using the formula weight. It comes out to
28.1 g NaCl. So the answer is that you would make the solution by dissolving 28.1 g NaCl in enough water to make 400 ml of solution.
There is also more than one way to do this problem. If you like the algebraic approach, you would write down the general equation shown in part a, substitute in the known values, solve for moles of NaCl, and then change that into grams.
Page 3 of 4
= 0.480 moles NaCl
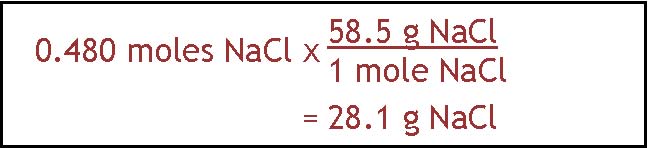
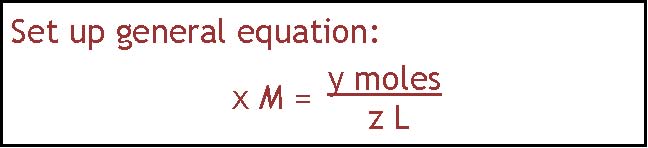
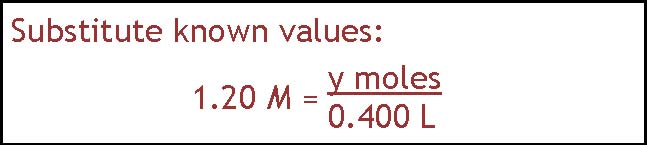
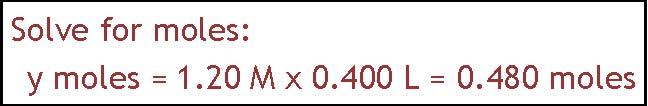
This question is a little easier. We do it the same way as the first step of the previous problem and then we stop. To find out how many moles of salt are contained in 300. ml of a 0.40 M NaCl solution, we start with the volume in liters (0.300 L) and multiply it by the number of moles per liter of solution, which is 0.40 moles over 1.00 L. The answer is 0.12 moles of NaCl. This could also have been done using algebra by writing down the general equation relating molarity, moles and liters, substituting the known values, and then solving the equation for moles.
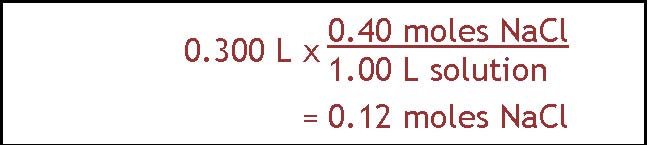
Now you should take some time to review the calculations above (ex. 3). If you have any
http://dl.clackamas.edu/ch105-04/calculat.htm 1/7/2011
Calculations Using Molarity Page 4 of 4
questions, check with your instructor. Once you are familiar with how those are done then you should try answering the following questions (exercise 4 in your workbook). Get help from the instructor if you need it. Check your answers below before you continue with the lesson.
What is the molarity of the solution?
How many moles of KBr are in 25.0 mL of a 1.23 M KBr solution?
Battery acid is generally 3 M H2SO4. Roughly how many grams of H2SO4 are in 400.
mL of this solution?
Here are the answers to exercise 4.
How would you prepare 100. mL of 0.25 M KNO3 solution? Dissolve 2.53 g of KNO3 What is the molarity of the solution? 0.324 M
How many moles of KBr are in 25.0 mL of a 1.23 M KBr solution?
0.0308 mol
Battery acid is generally 3 M H2SO4. Roughly how many grams of H2SO4 are in 400.
mL of this solution? 120 g
Top of Page
Back to Course Homepage
1/7/2011
E-mail instructor: Eden Francis
Clackamas Community College ©1998, 2003 Clackamas Community College, Hal Bender
http://dl.clackamas.edu/ch105-04/calculat.htm
Species Concentration Page 1 of 2
There are times when you need to deal with the concentration of chemical species in solution rather than the concentration of a chemical compound. Perhaps these examples will show why this is important.
When electrolytes dissolve in water, they
dissociate into ions. When sodium chloride
dissolves in water, sodium and chloride
ions are formed. When calcium chloride
dissolves in water, calcium and chloride
ions are formed. Note that different
amounts of chloride ions are formed. Equal
concentrations of NaCl and CaCl2 generate
different concentrations of Cl-ion.
With weak electrolytes, this issue is complicated by the fact that some of the chemical remains undissociated. For example when HF dissolves in water HF(aq), H+(aq) and F(aq) are all formed and present in the solution. Depending on the conditions under which the solution is formed, the concentration of each of those chemical species might be different.
When dealing with the concentrations of chemical species, it is customary to use brackets around the formula of the chemical specie as a symbol for the concentration of that specie. For example, [Cl-] = 2 M means the concentration of chloride ion is 2 M.
Later in this lesson (e.g. equilibrium constants) and in later lessons (e.g. reaction rates) we will need to focus on the concentration of the particular chemical species that are reacting with one another or of particular interest to us for some other reason. Molarity can be used for this. It is simply a matter of specifying that the concentration refers to a particular chemical specie rather than a chemical compound.
Top of Page
http://dl.clackamas.edu/ch105-04/species.htm
1/7/2011