Latest Works
Bouncing Jets


Numerical modeling of viscoelastic flows is of great importance for complex engineering applications involving blood, paints, adhesives or foodstuff. When considering viscoelastic flows, the velocity, pressure and stress must satisfy the mass and momentum equation, supplemented with a constitutive equation involving the velocity and stress.

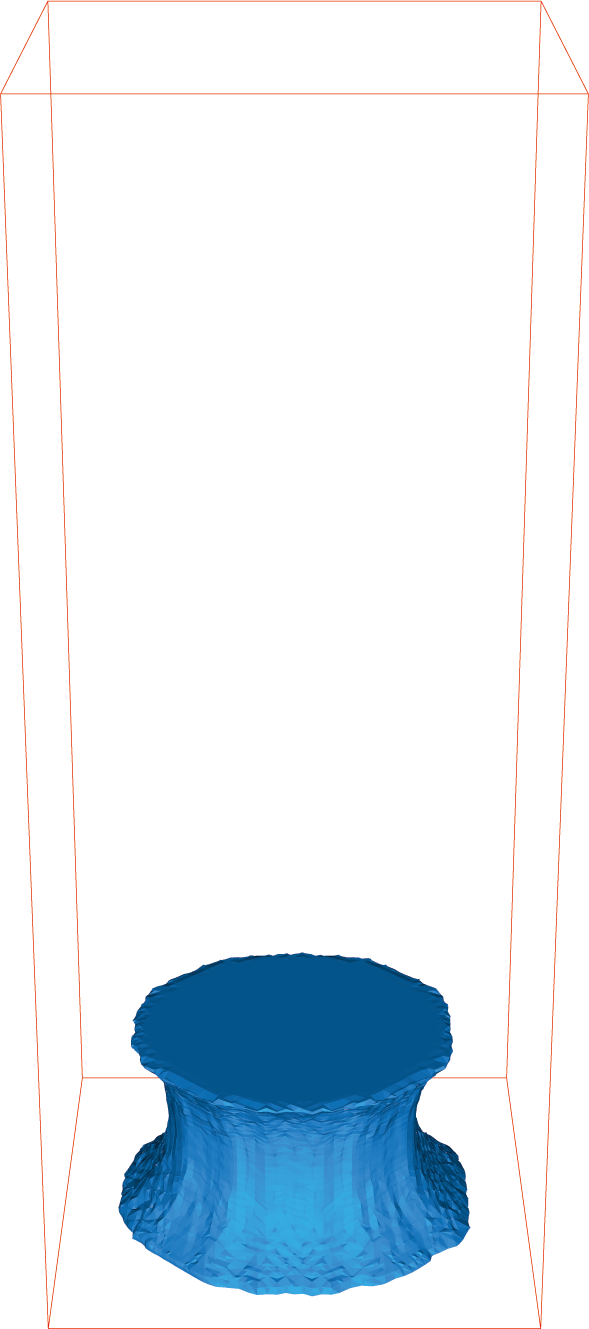

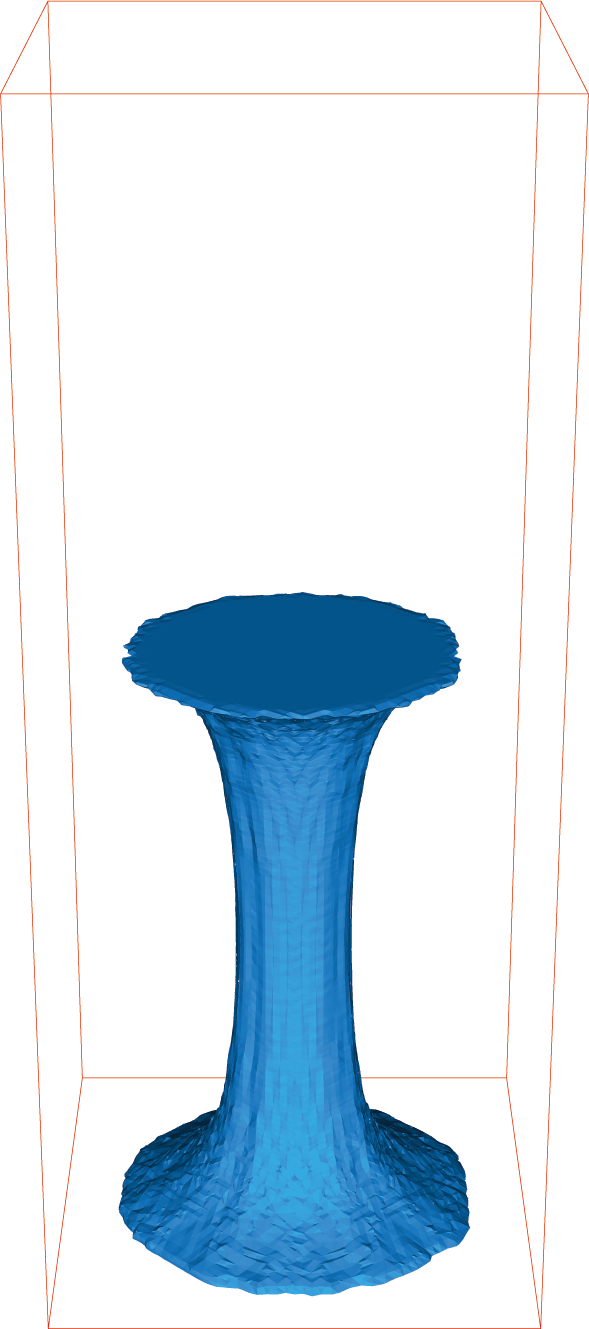
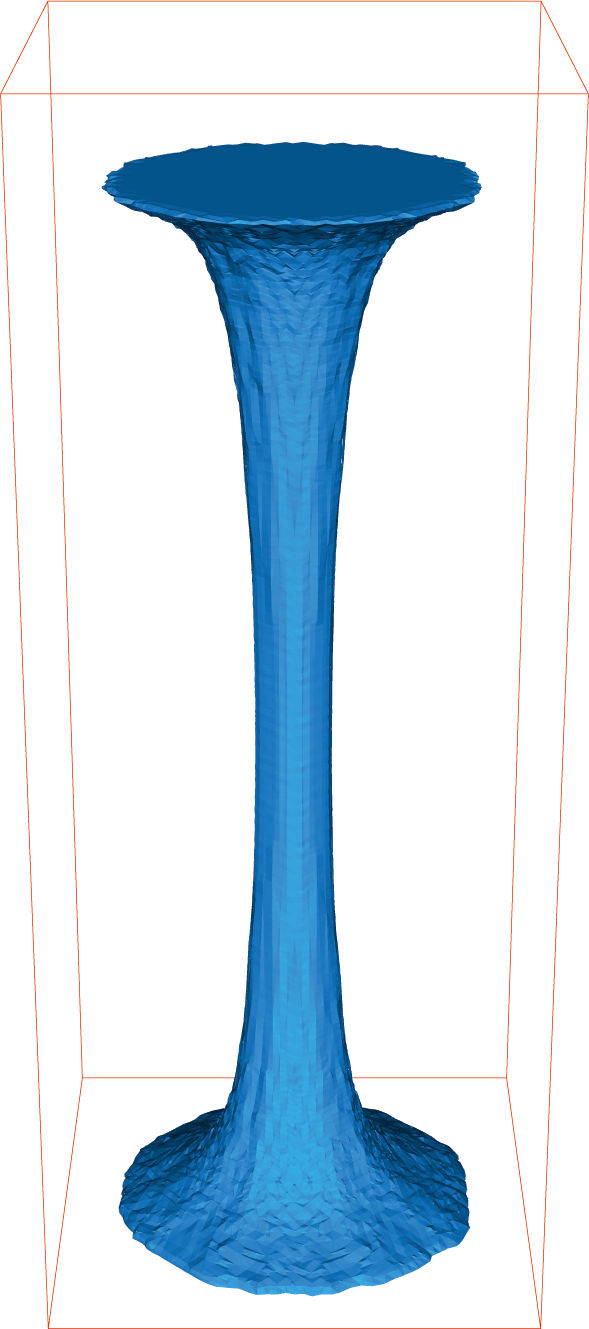 Stretching of a newtonian fluid
Stretching of a newtonian fluid

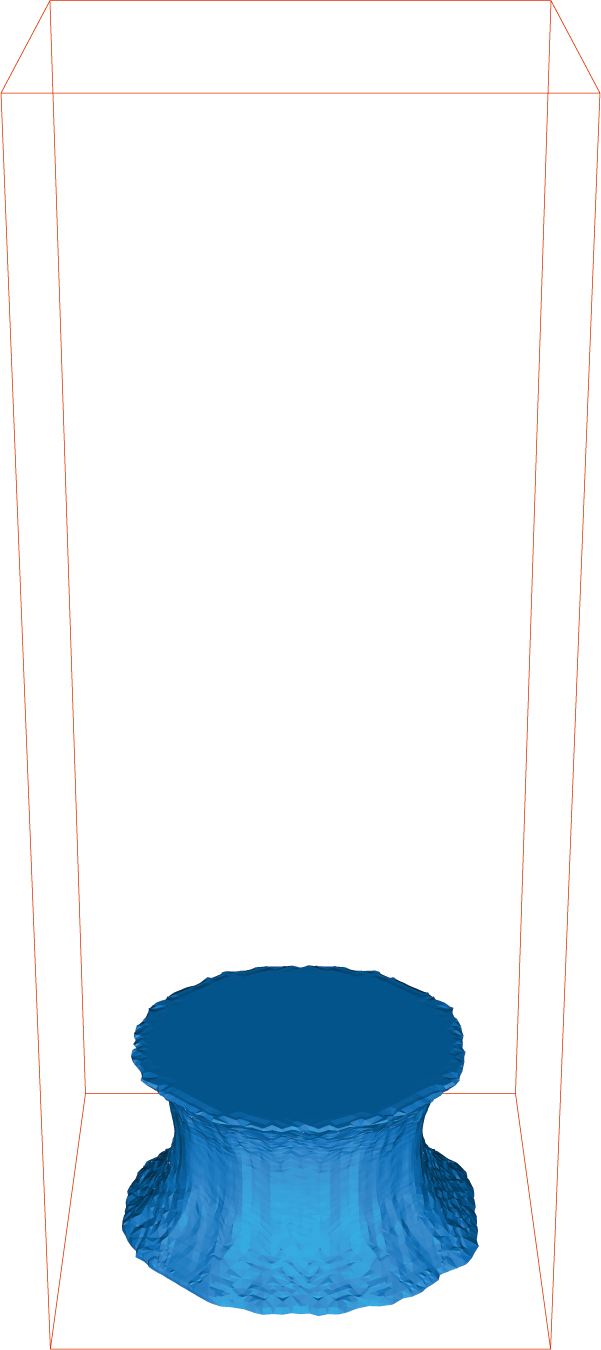
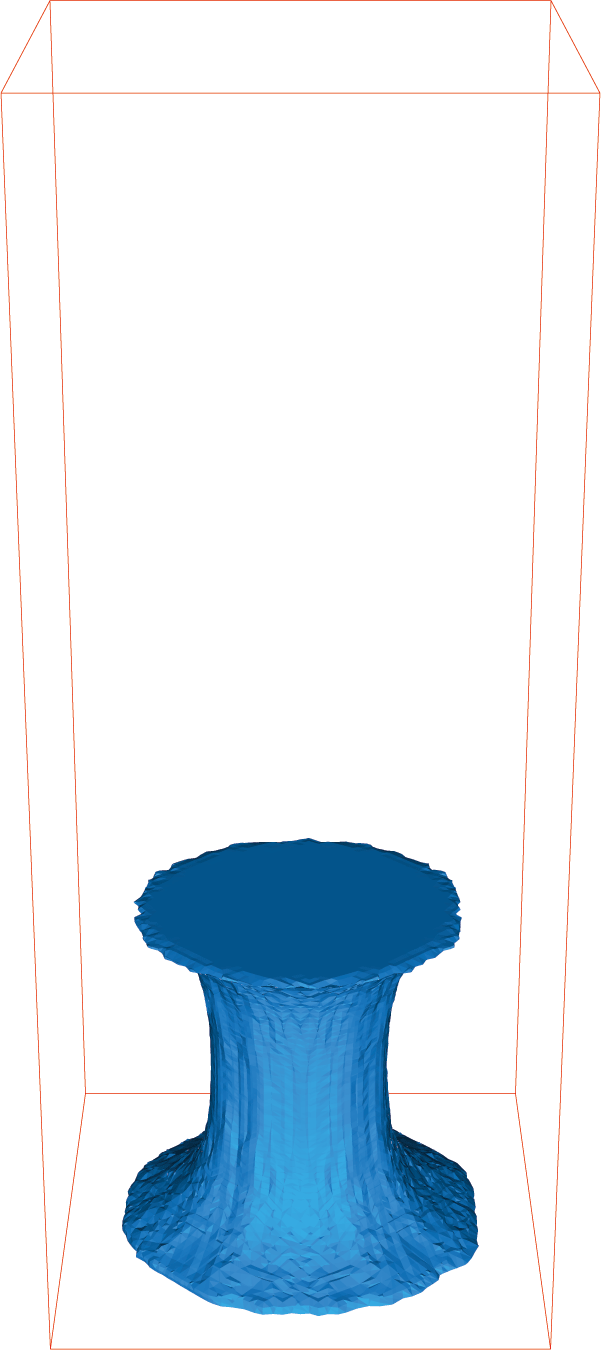
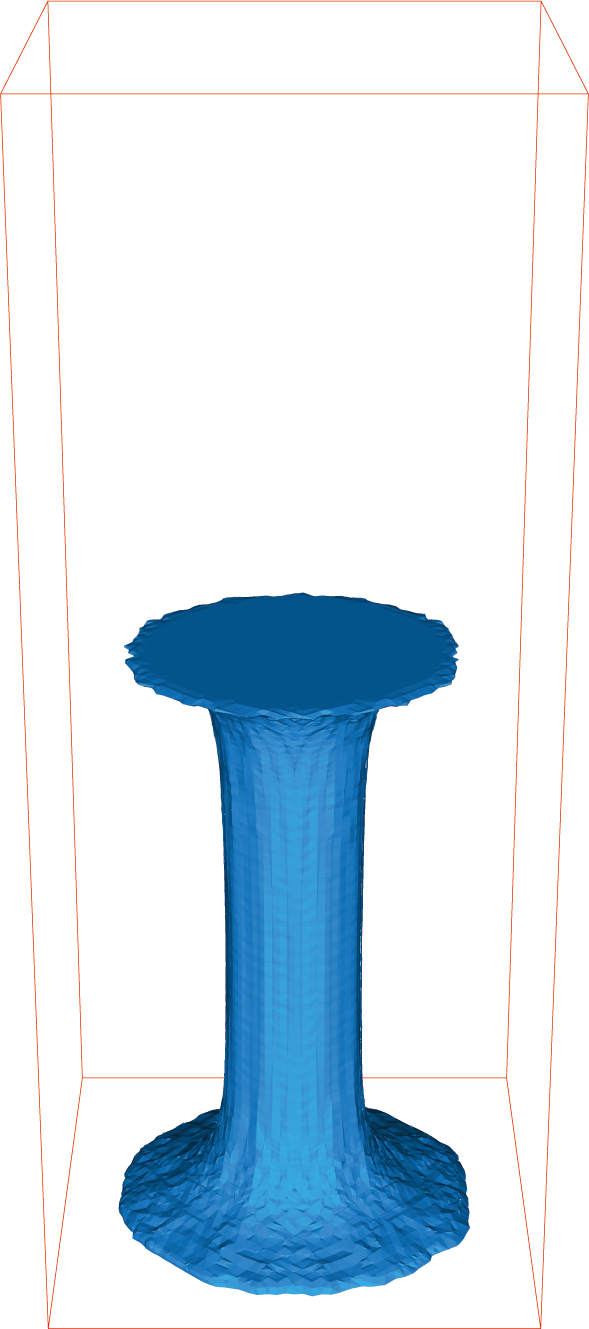
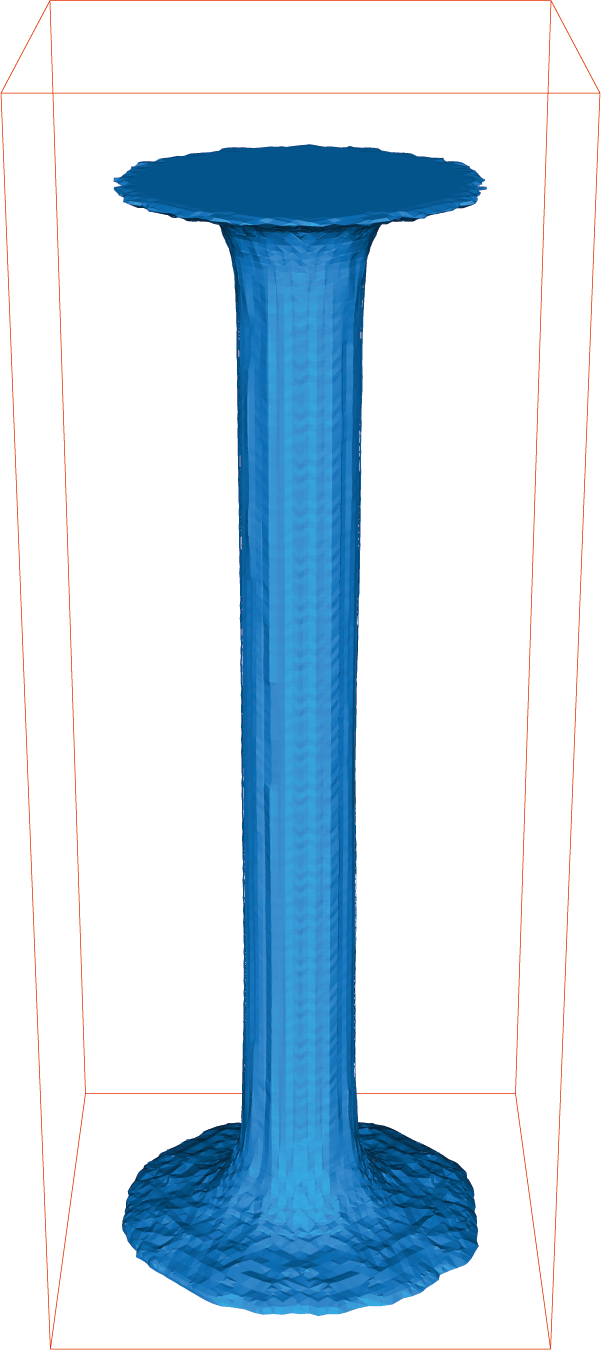 Stretching of a viscoelastic fluid
Stretching of a viscoelastic fluid
One of the simplest model is the so-called Oldroyd-B constitutive relation which can be derived from the kinetic theory of polymer dilute solutions.
In all cases reported below, the bouncing jets appear after a thin air layer is formed between the jet and the rest of the fluid. This air layer is sustained in the newtonian case by the bath horizontal velocity and in the shampoo case by its ability to shear-thinning.